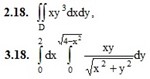DHS 13.1 - Option 18. Decisions Ryabushko AP
Content: 18v-IDZ13.1.pdf (106.60 KB)
Uploaded: 10.07.2025
Positive responses: 0
Negative responses: 0
Sold: 3
Refunds: 0
$1.39
1. Provide a double integral as an iterated integral with the outer integration over x and external integration with respect to y, if D is given the above lines.
1.18. D: y = √4 - x2, x ≥ 0, x = 1, y = 0.
2. Calculate the double integral over the region D, limited to lines.
D: y2 = 1 - x, x ≥ 0
3. Calculate the double integral using polar coordinates.
4. Calculate the area of a plane region D, bounded set tench.
4.18. D: y = -2x2 + 2, y ≥ - 6.
5. Use double integrals in polar coordinates to calculate the flat area of the figure bounded by the lines indicated.
5.18. (X2 + y2) 3 = a2x4
6. Calculate the volume of the body bounded by a given surface.
6.18. x2 = 1 - y, x + y + z = 3, y ≥ 0, z ≥ 0
1.18. D: y = √4 - x2, x ≥ 0, x = 1, y = 0.
2. Calculate the double integral over the region D, limited to lines.
D: y2 = 1 - x, x ≥ 0
3. Calculate the double integral using polar coordinates.
4. Calculate the area of a plane region D, bounded set tench.
4.18. D: y = -2x2 + 2, y ≥ - 6.
5. Use double integrals in polar coordinates to calculate the flat area of the figure bounded by the lines indicated.
5.18. (X2 + y2) 3 = a2x4
6. Calculate the volume of the body bounded by a given surface.
6.18. x2 = 1 - y, x + y + z = 3, y ≥ 0, z ≥ 0
Detailed solution. Designed in PDF format for easy viewing of IDZ solutions on smartphones and PCs. In MS Word (doc format) sent additionally.
No feedback yet