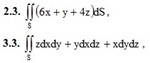DHS 15.1 - Option 3. Decisions Ryabushko AP
Content: 3v-IDZ15.1.pdf (113.21 KB)
Uploaded: 10.07.2025
Positive responses: 0
Negative responses: 0
Sold: 4
Refunds: 0
$1.28
1. Dana function u (M) = u (x, y, z) and the point M1, M2. Calculate: 1) The derivative of this function in the direction of the point M1 M1M2 vector; 2) grad u (M1)
1.3. u (M) = ln (x2 + y2 + z2), M1 (-1, 2, 1), M2 (3, 1, -1)
2. Calculate the surface integral of the first kind on the surface S, where S - part of the plane (p), cut off by the coordinate planes.
(P): 3x + 3y + z = 3
3. Calculate the surface integral of the second kind.
where S - the outer side surface of the cube bounded by the planes x = 0, y = 0, z = 0, x = 1, y = 1, z = 1
4. Calculate the flow vector field a (M) through the outer surface of the pyramid formed by plane (p) and the coordinate planes in two ways: a) determination using flow; b) using the formula Ostrogradskii - Gauss.
4.3. and (M) = xi + (x + z) j + (y + z) k, (p): 3x + 3y + z = 3
1.3. u (M) = ln (x2 + y2 + z2), M1 (-1, 2, 1), M2 (3, 1, -1)
2. Calculate the surface integral of the first kind on the surface S, where S - part of the plane (p), cut off by the coordinate planes.
(P): 3x + 3y + z = 3
3. Calculate the surface integral of the second kind.
where S - the outer side surface of the cube bounded by the planes x = 0, y = 0, z = 0, x = 1, y = 1, z = 1
4. Calculate the flow vector field a (M) through the outer surface of the pyramid formed by plane (p) and the coordinate planes in two ways: a) determination using flow; b) using the formula Ostrogradskii - Gauss.
4.3. and (M) = xi + (x + z) j + (y + z) k, (p): 3x + 3y + z = 3
Detailed solution. Designed in PDF format for easy viewing of IDZ solutions on smartphones and PCs. In MS Word (doc format) sent additionally.
No feedback yet